Registration and mosaicing of images have been in practice since long before the age of digital computers. Shortly after the photographic process was developed in 1839, the use of photographs was demonstrated on topographical mapping [1]. Images acquired from hill-tops or balloons were manually pieced together. After the development of airplane technology (1903) aerophotography became an exciting new field. The limited flying heights of the early airplanes and the need for large photo-maps, forced imaging experts to construct mosaic images from overlapping photographs. This was initially done by manually mosaicing [2] images which were acquired by calibrated equipment. The need for mosaicing continued to increase later in history as satellites started sending pictures back to earth. Improvements in computer technology became a natural motivation to develop computational techniques and to solve related problems.
The construction of mosaic images and the use of such images on several computer vision/graphics applications have been active areas of research in recent years. There have been a variety of new additions to the classic applications mentioned above that primarily aim to enhance image resolution and field of view. Image-based rendering [3] has become a major focus of attention combining two complementary fields: computer vision and computer graphics [4]. In computer graphics applications (e.g. [5]) images of the real world have been traditionally used as environment maps. These images are used as static background of synthetic scenes and mapped as shadows onto synthetic objects for a realistic look with computations which are much more efficient than ray tracing [6,7]. In early applications such environment maps were single images captured by fish-eye lenses or a sequence of images captured by wide-angle rectilinear lenses used as faces of a cube [5]. Mosaicing images on smooth surfaces (e.g. cylindirical [8,9,10] or spherical [11,12,13]) allows an unlimited resolution also avoiding discontinuities that can result from images that are acquired separately. Such immersive environments (with or without synthetic objects) provide the users an improved sense of presence in a virtual scene. A combination of such scenes used as nodes[8,13] allows the users to navigate through a remote environment. Computer vision methods can be used to generate intermediate views [14,9] between the nodes. As a reverse problem the 3D stucture of scenes can be reconstructed from multiple nodes [15,16,13,17,18]. Among other major applications of image mosaicing in computer vision are image stabilization [19,20], resolution enhancement [21,22], video processing [23] (e.g. video compression [24]. video indexing [25,26]).
The problem of image mosaicing is a combination of three problems:
Correcting geometric deformations using image data and/or camera models. Image registration using image data and/or camera models. Eliminating seams from image mosaics.

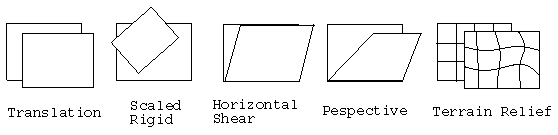
Some of the most common global transformations are affine, perspective and polynomial transformations. The first three cases of the Fig 1 are typical examples for the affine transformations. The remaining two are the common cases where perspective and polynomial transformations are used, respectively.
Having p = (x,y)T as old and p' = (x',y')T as the new coordinates of a pixel, a 2D affine transformation can be written as:










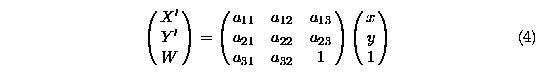

Alternatively, perspective transformations are often represented by the following equations known as homographies:




The 8-parameter homography accurately models a perspective transformation between different views for the case of a camera rotating around a nodal point. Such a perspective transformation is shown in Fig 2.a which displays a cross-section of the viewing sphere (i.e. a sphere of unit size with its center coinciding with the center of projection).
Fig 2 also illustrates some of the projective transformations that are alternative to the perspective transformation. Each of these projective transformations has distinctive features. Perspective transformations preserve lines whereas the stereographic transformations preserve circular shapes [29]. Stereographic transformations are capable of mapping a full field of view of the viewing sphere onto the projection plane. For the equi-distant projection (which can be viewed as flattening a spherical surface [30]) mapping a full field of view is no longer an asymptotical case. The distance between the point p* and the principle point c can be found according to the projection model:



A natural domain for representing and compositing images acquired by a camera rotating around its nodal point is a unit sphere centered at the nodal point. We use the term ``plenoptic image'' for an image composited on a spherical surface representing the entire 360o field of view. The term ``plenoptic'' was introduced by [32] and later popularized by [9]. A plenoptic function describes everything that is visible in radiant forms of energy to an observer for every possible location of the observer. A plenoptic image 2 is a sample of the plenoptic function for a fixed location of the observer.
Side views of cylindrical maps [8,9,10] are often chosen to represent plenoptic images compromising the discarded views of top and bottom with the uniform sampling in the cylindrical coordinate system. Uniform sampling feature is desirable especially when images are needed to be translated in the target domain. We use spherical surfaces (as in [11,12,13]) as an environment to construct plenoptic images. The construction of mosaic images on spherical surfaces is complicated by the singularities at the poles [33]. Numerical errors near the poles cause irregularities in the similarity measures used for automatic registration. Using images acquired with a fish-eye lens [12] and the small relative size of polar regions with respect to such images alleviates the negative effect of singularities. Relative rotational motions between image pairs are used in [13] (based on quaternions [34]) and [11] (based on an angular motion matrix [35]) before mapping images onto a sphere to avoid the effect of singularities in registration.
Images that form a large portion of a plenoptic image can be constructed on a single image frame by using special mirrors [36,37,38]. Having a single viewpoint [36,37] in such imaging systems is important for capability to reconstruct perspective views. Carefully calibrated and coupled mirrors [37] can capture two images that can be easily combined to form a plenoptic image. Even though this kind of approach provides a simple framework for capturing a full field of view of a scene, the limited resolution of the film frame (or sensor array) may be a serious limitation for recording images in detail. Plenoptic images constructed by mosaicing smaller images can store detailed information without being subject to such limits.
The complications due to parallax that are observed in the case of translational motion of a planar camera can be avoided by using a one dimensional camera (i.e. ``pushbroom camera'') to scan scenes. This action can be emulated using conventional cameras by combining strips taken from a sequence of two dimensional images as a series of neighboring segments. These cameras can directly acquire cylindrical (with a rotating motion) and orthographic (with translational motion) maps [39]. They can also acquire images along an arbitrary path [40].
The strips that should be taken from two dimensional images are identified as the ones perpendicular to the image flow in [41]. These family of strips can handle a wide variety of motions including forward motion and optical zoom. Additional formulation is developed in [42] for these complicated cases of motion.
Images acquired as a combination of strips (along with range images and a recorded path of camera) are also shown to be effective in complete 3D reconstruction of scenes [43].
Polynomial transformations are often referred to as ``rubber sheet transformations'' [44] to describe their capability to change shapes of objects until they appear to be in desired shape. Using only correspondences of image points they can handle global distortions (e.g. pincushion/barrel distortion) which can not be modeled easily as in perspective transformations. A bivariate polynomial transformation is of the form:



Irani et al. [25,46,23,24] choose to use polynomial transformations with more degrees of freedom than the 8-parameter bilinear transformation that can accurately handle perspective distortions. They use the extra degrees of freedom in the transformation to deal with the nonlinearities due to parallax, scene change etc.
Global transformations described above impose a single mapping function on the image. They do not account for (with the exception of weighted least squares solution) local variations. Local distortions may be present in scenes due to a motion parallax, movement of objects etc.
The parameters of a local mapping transformation vary across the different regions of the image to handle local deformations. One way to do this is to partition the image into smaller sub-regions such as triangular regions with corners at the control points and then find a linear [47] transformation that exactly maps corners to desired locations. Smoother results can be obtained by a nonlinear transformation [48]. In [49] the control points are selected to be along the desired border of overlapping images. A transformation that relocates these points to align with their correspondences has an effect on rest of the pixels inversely proportional to their distances to the control points. In [50] local variations that need to be corrected are estimated by the image flow between corresponding images that have undergone global transformations.
Although the local transformations can correct deformations that are not corrected by global corrections it is difficult to justify their necessity in image mosaicing. Warping images simply to reduce local variations (e.g. aligning a moving object by warping its local neighborhood) is likely to introduce unnatural distortions in the warped areas. We address the problem of local distortions during the mosaicing process by minimizing their significance in the blended images.
A detailed discussion on spatial transformation and interpolation methods can be found in [45].
Image registration is the task of matching two or more images. It has been a central issue for a variety of problems in image processing [51] such as object recognition, monitoring satellite images, matching stereo images for reconstructing depth, matching biomedical images for diagnosis, etc.
Registration is also the central task of image mosaicing procedures. Carefully calibrated and prerecorded camera parameters may be used to eliminate the need for an automatic registration. User interaction also is a reliable source for manually registering images (e.g. by choosing corresponding points and employing necessary transformations on screen with visual feedback). Automated methods for image registration used in image mosaicing literature can be categorized as follows:
Feature based [52,27] methods rely on accurate detection of image features. Correspondences between features lead to computation of the camera motion which can be tested for alignment. In the absence of distinctive features, this kind of approach is likely to fail.
Exhaustively searching for a best match for all possible motion parameters can be computationally extremely expensive. Using hierarchical processing (i.e. coarse-to-fine [53]) results in significant speed-ups. We also use this approach also taking advantage of parallel processing [31] for additional performance improvement.
Frequency domain approaches for finding displacement [54] and rotation/scale [55,56] are computationally efficient but can be sensitive to noise. These methods also require the overlap extent to occupy a significant portion of the images (e.g. at least 50%).
Iteratively adjusting camera-motion parameters leads to local minimums unless a reliable initial estimate is provided. Initial estimates can be obtained using a coarse global search or an efficiently implemented frequency domain approach [28,18].
Images aligned after undergoing geometric corrections most likely require further processing to eliminate remaining distortions and discontinuities. Alignment of images may be imperfect due to registration errors resulting from incompatible model assumptions, dynamic scenes, etc. Furthermore, in most cases images that need to be mosaiced are not exposed evenly due to changing lighting conditions, automatic controls of cameras, printing/scanning devices, etc. These unwanted effects can be alleviated during the compositing process.
The main problem in image compositing is the problem of determining how the pixels in an overlapping area should be represented. Finding the best separation border between overlapping images [57] has the potential to eliminate remaining geometric distortions. Such a border is likely to traverse around moving objects avoiding double exposure [56,30]. The uneven exposure problem can be solved by histogram equalization [30,58], by iteratively distributing the edge effect on the border to a large area [59], or by a smooth blending function [60].
We expect the use of image mosaicing to make a significant impact in video processing [23]. The complete representation of static scenes resulting from mosaicing video frames in conjunction with an efficient representation for dynamic changes provide a versatile environment for visualizing, efficiently coding, accessing, analyzing information. Besides video compression [24] and indexing [25,26] this environment is shown to be useful for image stabilization [19,20] and building high quality images using low-cost imaging equipments [21,22].
As indicated by the recent history of newly developed applications, image mosaicing has become a major field of research. Besides a growing number of research papers, the public interest in image mosaicing has also been substantial. In recent years several constructing tools and viewers for panoramic images have appeared as successful commercial products such as Adessosoft Inc.'s PanoTouch©, Apple's Quicktime VRTM [8], Black Diamond Inc.'s Surround Video©, Terran Interactive Inc.'s Electrifier Pro©, Enroute Imaging's Quickstich©, IBM's PanoramIX©, Infinite Pictures' SmoothMoveTM, Interactive Pictures' IPIXTM Multimedia Builder, Live Picture Inc.'s PhotoVistaTM, Panavue's Visual SticherTM, PictureWorks' Spin Panorama©, RealSpace Inc.'s RealVRTM, RoundAbout Logic's Nodester©, Ulead Systems' Cool 3D©, Videobrush Corp.'s Panorama© [65], Visdyn's JutvisionTM .
1 Four point correspondences are sufficient to solve for eight unknown parameters
2 McMillan and Bishop [9] use the term ``plenoptic sample''.
© 1999 Sevket Gumustekin, All Rights Reserved.